展開とは
展開とは、掛け算の形を足し算や引き算の形に変えることです。
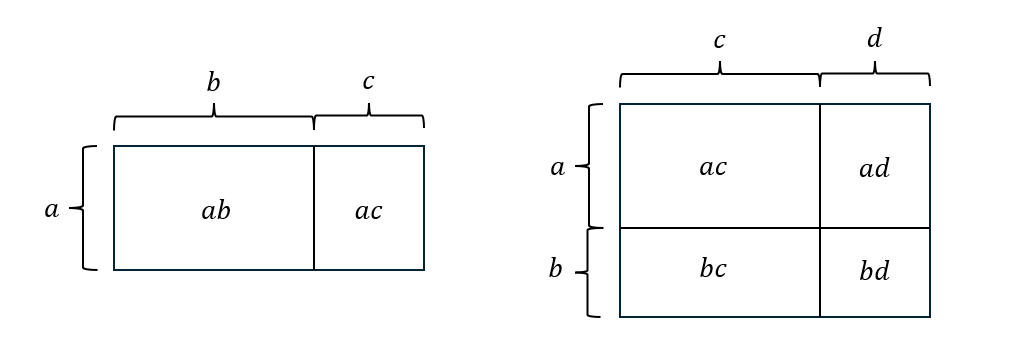
左側の図を見てください。大きい長方形が左右に2分割されています。 大きい長方形の面積は縦の長さが \(a\) で横の長さが \(b+c\) です。つまりこの長方形の面積は \(a(b+c)\) となります。 一方で、全体の長方形が2分割された長方形の面積は左が \(ab\) で右が \(ac\) です。 よって全体の面積は \(ab+ac\) となります。 これらはどちらも同じ面積なので次の式が成り立ちます。
式の左辺は掛け算の形、右辺は足し算の形で表されています。 左辺から右辺へのような式の変換を展開といいます。 毎回図を描いて面積を求めると大変なので、普段は次のプロセスで展開をしましょう。:
- まず、括弧の外にある項 \(a\) を、括弧の中の各項に掛けます。
- 具体的には、 \(a\) を括弧の中の最初の項 \(b\) に掛けて \(ab\) を得ます。
- 次に、同じ \(a\) を括弧の中の次の項 \(c\) に掛けて \(ac\) を得ます。
- 最後に、これらの結果を全て足し合わせることで、展開された形が得られます。
次に右側の図を見てください。先ほどと同様に全体の面積と4分割された面積の和から次の式が得られます。
この展開は次のプロセスで求めましょう。:
- まず、最初の括弧の最初の項 \(a\) を、二つ目の括弧のそれぞれの項 \(c\) と \(d\) に掛けます。これにより、最初の二項 \(ac\) と \(ad\) が得られます。
- 次に、最初の括弧の二つ目の項 \(b\) を、同じく二つ目の括弧のそれぞれの項 \(c\) と \(d\) に掛けます。これにより、次の二項 \(bc\) と \(bd\) が得られます。
- 最後に、これらの結果を全て足し合わせることで、展開された形が得られます。
したがって、元の形 \((a + b)(c + d)\) を展開すると、\(ac + ad + bc + bd\) になります。
ちなみに、この式の導出は置き換えでもできます。\(a+b=X\)とすると、先ほどの式から \(X(c+d)=Xc+Xd\) となります。次に \(X=a+b\) を使って置き換えをもとに戻すと、\((a+b)c+(a+b)d\) となり、これを展開すると \(ac+bc+ad+bd\) が得られます。
では、図を描いたり置き換えを使って次の式を展開してみましょう。
\((a+b)(c+d+e)=\)
\((a+b)(c+d)(e+f)=\)
\((x+1)(x+2)=\)
足し算の順番は異なっていてもOKです。
因数分解とは
因数分解は、展開の逆です。つまり、足し算や引き算の形を掛け算の形に変えることです。
この式の左辺から右辺の形に変えるのが因数分解です。
しかし、展開とは少し難しい点があります。例えば、展開の最後の問題、\((x+1)(x+2)\) を考えてみてください。
最後の過程で \(2x+x=3x\) の計算が行われました。因数分解では \(3x\) が \(2x+x\) の計算由来であることを
求めなければいけないのです。これが因数分解が一筋縄ではいかない最大の理由です。
では、一般的な因数分解の手順を説明します。
- 共通因数でくくる
- 公式に当てはめる
- 次数が低い文字に着目し、再度1・2の手順を行う
1.共通因数でくくる
共通の文字や、最大公約数でくくります。共通因数とは、すべての式を同時に割り切ることのできる数です。 例えば、\(4a^3b-6a^2bc\) は4と6の最大公約数である「2」と、 \(a^2b\) が共通因数であるため次のように因数分解できます。2.公式に当てはめる
公式集に当てはまる形の場合、その公式に代入することで因数分解ができます。例えば \(x^2+5x+4\) の因数分解を考えてみましょう。これは公式集4.\((x+a)(x+b)=x^2+(a+b)x+ab\) の右辺と同じ形をしています。 係数に着目すると \(a+b=5, ab=4\) が与えられた式です。 つまり、\(a+b=5, ab=4\) を満たす \(a,b\) を探すのです。 和が5で積が4の2つの数は1と4なので、\(a=1,b=4\) が得られます(\(a\)と\(b\)は逆でも可)。 よって、公式集4.\((x+a)(x+b)=x^2+(a+b)x+ab\) に \(a=1,b=4\) を代入すると、次のように因数分解ができます。
次に、\(2x^2-3x-2\) の因数分解を考えてみましょう。これは公式集5.\((ax+b)(cx+d)=acx^2+(ad+bc)x+bd\) をもとに考えます。 先ほどと同様に考えると、\(ac=2, ad+bc=-3, bd=-2\) を満たす \(a,b,c,d\) を求めることになります。 この方程式の解き方は \(ac=2, bd=-2\) を満たす組(多くの場合、整数)を探します。その中で \(ad+bc=-3\) を満たす組が見つかれば成功です。 今回のケースでは \(a=2, b=1, c=1, d=-2\) なので次のように因数分解されます。
最後に、\(x^2-4\) の因数分解を考えてみましょう。これは公式集3.\((a+b)(a-b)=a^2-b^2\) をもとに考えます。 この「2乗-2乗」の計算はとてもよく使うので絶対に覚えておきましょう!!!この場合、\(a=x, b=2\) なので次のように因数分解されます。
3.次数が低い文字に着目する
複数の文字が混在する式を因数分解しなければならない場合、各文字ごとの次数を考えると因数分解が可能です。 例えば、\(a^2+ab+a+b\) の因数分解を考えてみましょう。この式は文字 \(a\) に着目すると2次式、文字 \(b\) に着目すると1次式です。 つまり、文字 \(b\) に着目してこの式をまとめます。\(a^2+ab+a+b=b(a+1)+(a^2+a)\)
まとめた後、部分的に因数分解ができる項は因数分解をします。
\(b(a+1)+(a^2+a)=b(a+1)+a(a+1)\)
すると共通因数の \(a+1\) が求められました。よってこの因数分解の結果は次のようになります。
なお、すべての文字が同じ次数の場合でも、いずれか一つの文字に着目すると因数分解ができる可能性が高いです。
最後に紹介したやり方では因数分解が困難で、多少のやり方の暗記が必要なケースを紹介します。
- 2乗-2乗の形にするパターン
- 覚えるしかない問題
公式集
左辺から右辺への変換が展開、右辺から左辺の変換が因数分解です。すべて覚えましょう。
- \((a+b)^2=a^2+2ab+b^2\)
- \((a-b)^2=a^2-2ab+b^2\)
- \((a+b)(a-b)=a^2-b^2\)
- \((x+a)(x+b)=x^2+(a+b)x+ab\)
- \((ax+b)(cx+d)=acx^2+(ad+bc)x+bd\)
- \((a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca\)
- \((a+b)^3=a^3+3a^2b+3ab^2+b^3\)
- \((a-b)^3=a^3-3a^2b+3ab^2-b^3\)
- \((a+b)(a^2-ab+b^2)=a^3+b^3\)
- \((a-b)(a^2+ab+b^2)=a^3-b^3\)